11609. Finding pairs
A tree with n vertices is given.
Vertex 1 is considered the root. There is exactly one simple path between any
two vertices.
Let d(i, j) denote the number of edges on the path from vertex i
to vertex j.
Find the number of vertex pairs (i, j) such that the following equality holds:
d(i, j) = d(i, 1) – d(j, 1)
Input. The first line contains a single integer n (1 ≤ n ≤ 105) – the number of vertices in the tree.
Each of the next n
– 1 lines contains two integers, describing the
edges of the tree: the pairs of vertices connected by an edge.
Output. Print a single integer – the
number of pairs (i, j) for which d(i, j) = d(i, 1) – d(j, 1) holds.
|
Sample
input |
Sample
output |
|
5 1 2 2 3 2 4 4 5 |
13 |
SOLUTION
graphs – depth first
search
Algorithm analysis
The condition d(i, j) = d(i, 1) – d(j, 1) holds for every pair of vertices (i, j) where j is an
ancestor of i in the depth-first search starting from vertex 1.
Let us consider an
example:
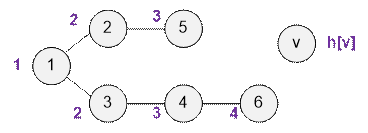
·
d(4, 1) = 2, d(4, 1) – d(1, 1) = 2 – 0 = 2;
·
d(6, 3) = 2, d(6, 1) – d(3, 1) = 3 – 1 = 2;
·
d(2, 2) = 0, d(2, 1) – d(2, 1) = 1 – 1 = 0;
·
d(6, 1) = 3, d(6, 1) – d(1, 1) = 3 – 0 = 3;
Let us define the depth
h[v] of a vertex v as
the number of vertices on the path from the root (vertex 1) to v. In the
diagram, the depth is written next to each vertex.
Now, fix a vertex i
and ask the question: how many vertices j are there such that the
condition d(i, j) = d(i, 1) – d(j, 1) is satisfied?
For example, for i = 6, there are
4 such vertices: j = 1, 3, 4, 6. Note that h[6] = 4. Thus, for a fixed vertex i, there
are exactly h[i] suitable vertices j.
To solve the
problem, we need to compute the depth h[v] for each vertex v in
the tree, and then find the sum of all these depths across the tree.
Example
Let us consider the graph from the example.
Next to each vertex, we write its depth.
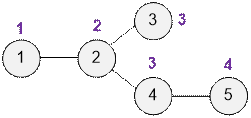
The sum of the
depths of all vertices is 1 + 2 + 3 + 3 + 4 = 13.
Algorithm implementation
Define
the graph’s adjacency list as g. The depths of the vertices are stored
in the array h.
vector<vector<int> > g;
vector<int> h;
The
dfs function computes the depth of each vertex v. The
parent of vertex v is the vertex p.
int dfs(int v, int p)
{
for (int to : g[v])
Consider
the edge (v, to). If the vertex to is not the parent of
vertex v, compute its depth and perform a depth first search starting from
it.
if (to != p)
{
h[to] = h[v] + 1;
dfs(to, v);
}
return h[v];
}
The
main part of the program. Read the number of vertices n in the tree.
scanf("%d", &n);
g.resize(n + 1);
Construct
a tree.
for (i = 2; i <= n; i++)
{
scanf("%d %d", &a,
&b);
g[a].push_back(b);
g[b].push_back(a);
}
Set
the depth of vertex 1 to be 1.
h.resize(n + 1);
h[1] = 1;
Start
a depth first search from the vertex 1.
dfs(1, -1);
Compute
the answer – the sum of the depths of all vertices.
res = 0;
for (i = 1; i <= n; i++)
res += h[i];
Print
the answer.
printf("%lld\n", res);